Monty Hall Problem

Monty Hall Problem

The Monty Hall Problem is a simple problem that has stumped many of the smartest people. In this problem there is a host and a player. There are three doors. Two doors contain goats and one door contains a car. Your goal is to achieve that car. The host of the game already knows which door has which object. You first choose one of the doors. The host will then reveal one door from the remaining two doors and the door he reveals must have a goat. You are given a choice to switch to the other door or stay with your original choice. The question is, will you switch?

Most people think that once the host has revealed a door with a goat in it, that the other two doors have a half-half chance of containing the car and that it doesn't matter whether or not you switch doors. However, this is a common misconception.

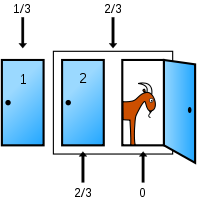
Let's say you pick door 1. Your first choice will have a 1/3 probability of being the car. There is a likelihood of 2/3 that the car is in door 2 and door 3. However, once the host reveals door 3 that is goat. The probability of the car being in the door 3 is 0 and the 2/3 probability is shifted to door 2. Now, door 2 has a 2/3 probability of containing the car while door 1 only has a 1/3 probability of containing the car. Thus, you should always switch doors.

To actually visualize this problem better, let's build a simulation.

I'm going to build a class called Monty Hall to simulate one round of the game.

class Monty_Hall:

    def __init__(self):
        self.game = ['car', 'goat', 'goat']
        # position of choice
        self.choice_pos = None
        # position of monty's choice
        self.monty_choice_pos = None
        # doors you can choose from
        self.options = range(0, 3)
        # shuffle the doors
        random.shuffle(self.game)
        # doors monty can choose from
        self.monty_options = [door_num for door_num in range(0, 3)
                          if self.game[door_num] == 'goat']

The first thing in this game is that the player needs to choose a certain door.

    def choose(self, door_pos):
        self.choice_pos = door_pos
        try:
            self.monty_options.remove(self.choice_pos)
        except ValueError:
            pass
        self.options.remove(self.choice_pos)

I assign the door position parameter of this method into the variable of the position of my choice and removes that choice from my options.

The second thing in this game is for Monty to reveal one of the other two doors that has a goat in it.

    def monty_choose(self):
        self.monty_choice_pos = random.choice(self.monty_options)
        self.options.remove(self.monty_choice_pos)

Now the player is offered a choice to switch to a different door.

There are three strategies:

1. The player always stays with his original choice
2. The player always switch from his original choice to the other door
3. The player randomly decide whether or not to switch doors

    def stay(self):
        pass

    def switch(self):
        self.choice_pos = random.choice(self.options)
        self.options.remove(self.choice_pos)

    def random_switch(self):
        if random.random() < 0.5:
            self.switch()

Now, I create a function to simulate the play of this game one time with the specified strategy and outputs whether the player achieve the car or not.

def simulate(strategy):
    a = Monty_Hall()
    a.choose(random.choice(range(0, 3)))
    a.monty_choose()
    if strategy == 'stay':
        a.stay()
    elif strategy == 'switch':
        a.switch()
    elif strategy == 'random':
        a.random_switch()
    if a.game[a.choice_pos] == 'car':
        return True
    else:
        return False

Lastly, I create a function to run this simulation many times and compare the rate of winning the car for each strategy.

def run_simulation(num_times):
    results = {'stay_wins': 0, 'stay_losses': 0,
               'switch_wins': 0, 'switch_losses': 0,
               'random_wins': 0, 'random_losses': 0}
    for i in range(0, num_times):
        for strat in ['stay', 'switch', 'random']:
            if simulate(strat):
                results[strat + '_wins'] += 1
            else:
                results[strat + '_losses'] += 1

    for strat in ['stay', 'switch', 'random']:
        print strat + ' win ratio: ' + str(results[strat+'_wins']/float(num_times))

Let's run this code on the console.

>>> run_simulation(1000)
stay win ratio: 0.332
switch win ratio: 0.675
random win ratio: 0.505

As you can see, the rate of success if you always stay with your original choice is about 33% (1/3).
The rate of success if you randomly choose between staying and switching doors is about 50% (1/2).
The rate of success if you always switch to the last door is about 66% (2/3).

COMPLETE PROGRAM

import random

class Monty_Hall:

    def __init__(self):
        self.game = ['car', 'goat', 'goat']
        # position of choice
        self.choice_pos = None
        # position of monty's choice
        self.monty_choice_pos = None
        # doors you can choose from
        self.options = range(0, 3)
        # shuffle the doors
        random.shuffle(self.game)
        # doors monty can choose from
        self.monty_options = [door_num for door_num in range(0, 3)
                          if self.game[door_num] == 'goat']

    def choose(self, door_pos):
        self.choice_pos = door_pos
        try:
            self.monty_options.remove(self.choice_pos)
        except ValueError:
            pass
        self.options.remove(self.choice_pos)

    def monty_choose(self):
        self.monty_choice_pos = random.choice(self.monty_options)
        self.options.remove(self.monty_choice_pos)

    def stay(self):
        pass

    def switch(self):
        self.choice_pos = random.choice(self.options)
        self.options.remove(self.choice_pos)

    def random_switch(self):
        if random.random() < 0.5:
            self.switch()

def simulate(strategy):
    a = Monty_Hall()
    a.choose(random.choice(range(0, 3)))
    a.monty_choose()
    if strategy == 'stay':
        a.stay()
    elif strategy == 'switch':
        a.switch()
    elif strategy == 'random':
        a.random_switch()
    if a.game[a.choice_pos] == 'car':
        return True
    else:
        return False

def run_simulation(num_times):
    results = {'stay_wins': 0, 'stay_losses': 0,
               'switch_wins': 0, 'switch_losses': 0,
               'random_wins': 0, 'random_losses': 0}
    for i in range(0, num_times):
        for strat in ['stay', 'switch', 'random']:
            if simulate(strat):
                results[strat + '_wins'] += 1
            else:
                results[strat + '_losses'] += 1

    for strat in ['stay', 'switch', 'random']:
        print strat + ' win ratio: ' + str(results[strat+'_wins']/float(num_times))